Persamaan Kuadrat - Bentum Umum, dan Cara Menyelesaikan Persamaan Kuadrat
Persamaan kuadrat adalah persamaan yang memuat variabel berpangkat dengan pangkat tertingginya sama dengan dua (2).
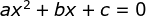
2. Penyelesaian Persamaan Kuadrat
a). Menfaktorkan
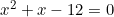
b). Melengkapkan Kuadrat Sempurna
^{2}=x^{2}+2ax+a^{2})
^{2}=x^{2}-2ax+a^{2})
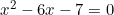
c). Menggunakan Rumus ABC
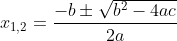
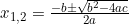
}}{2.2})
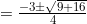
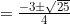
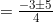
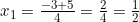
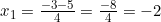
Contoh:
a. 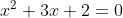
b. 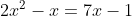
Kedua persamaan kuadrat tersebut mempunyai bentuk yang berbeda-beda. Dalam hal ini, kedua persamaan kuadrat tersebut dapat diubah ke dalam bentuk umum. Persamaan kuadrat mempunyai bentuk umum sebagai berikut:
dengan a ≠ 0 dan a, b, c ϵ R.
2. Penyelesaian Persamaan Kuadrat
Nilai x yang memenuhi persamaan kuadrat 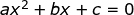 disebut akar-akar persamaan. Proses menentukan akar-akar persamaan kuadrat dinamakan menyelesaikan persamaan kuadrat. Persamaan kuadrat dapat diselesaikan dengan tiga (3) cara sebagai berikut:
disebut akar-akar persamaan. Proses menentukan akar-akar persamaan kuadrat dinamakan menyelesaikan persamaan kuadrat. Persamaan kuadrat dapat diselesaikan dengan tiga (3) cara sebagai berikut:
Agar dapat difaktorkan, persamaan kuadrat harus diubah sedemikian rupa sehingga ruas kanan sama dengan nol (0). Selanjutnya, ruas kiri diubah menjadi perkalian dua (2) suku linear.
Contoh:
Tentukan himpunan penyelesaian dari persamaan kuadrat 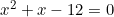 menggunakan cara memfaktorkan.
menggunakan cara memfaktorkan.
Penyelesaian:
⇔ (x - 3) . (x + 4)
⇔ x - 3 = 0 atau x + 4 = 0
⇔ x = 3 atau x = - 4
Jadi, HP = { -4, 3 }
Kuadrat sempurna mempunyai bentuk umum sebagai berikut.
Proses penambahan kedua ruas agar menjadi bentuk kuadrat sempura dinamakan melengkapkan kuadrat.
Contoh:
Tentukan himunan penyelesaian dari persamaan kuadrat 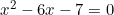 menggunakan cara melengkapkan kuadrat sempurna.
menggunakan cara melengkapkan kuadrat sempurna.
Penyelesaian:
⇔ 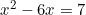
⇔ ^{2}=7+(-3)^{2})
⇔ 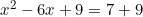
⇔ ^{2}=16)
⇔ 
⇔ 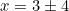
⇔ 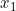 = 3 + 4 = 7 atau
= 3 + 4 = 7 atau 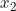 = 3 - 4 = -1
= 3 - 4 = -1
Jadi, HP = { -1, 7 }
Akar-akar persamaan kuadrat 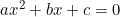 dapat ditentukan menggunakan rumus ABC sebagai berikut.
dapat ditentukan menggunakan rumus ABC sebagai berikut.
Contoh:
Tentukan himpunan penyelesaian dari persamaan kuadrat 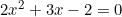 mengunakan rumus ABC.
mengunakan rumus ABC.
Penyelesaian:
Persamaan kuadrat 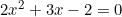
Berarti, a = 2, b = 3, dan c = -2.
Dengan Demikian,
Maka:
Jadi, HP { 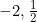 }
}

