Fungsi Trigonometri : Enam Fungsi Trigonometri Dasar dan Identitas Trigonometri
Enam Fungsi Trigonometri Dasar


Rumus diatas dapat diperluas menjadi sebagai berikut:


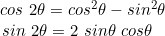
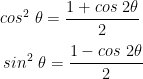
d). Hukum Kosinus
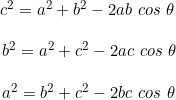
Jawab:
1. cos (x - ) = cos x. cos
) = cos x. cos  + sin x. sin
+ sin x. sin 
= cos x . 0 + sin x. 1
= 0 + sin x
= sin x
2. sin (x + ) = sin x.cos
) = sin x.cos  + cos x. sin
+ cos x. sin 
= sin x. 0 + cos x. 1
= 0 + cos x
= cos x
3. cos (x + ) = cos x. cos
) = cos x. cos  - sin x. sin
- sin x. sin 
= cos x . 0 - sin x. 1
= 0 - sin x
= -sin x
4. sin (x - ) = sin x.cos
) = sin x.cos  + cos x. sin
+ cos x. sin 
= sin x. 0 - cos x. 1
= 0 - cos x
= -cos x
Contoh 1.2
Berikut ini adalah contoh rumus setengah sudut. Carilah nilai fungsi berikut!

Jawab:






Rumus diatas dapat diperluas menjadi sebagai berikut:

Identitas Trigonometri

a). Rumus Penjumlahan 2 Sudut
cos (A + B) = cos A.cos B - sin A.sin B
cos (A - B) = cos A.cos B + sin A.sin B
sin (A + B) = sin A.cos B + cos A.sin B
sin (A - B) = sin A.cos B - cos A.sin B
Dari hubungan rumus cos^2 + sin^2
+ sin^2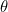 = 1 dengan rumus penjumlahan maka akan didapat rumus berikut ini.
= 1 dengan rumus penjumlahan maka akan didapat rumus berikut ini.
b). Rumus Sudut-Ganda
Dan Rumus penjumlahan sendiri berasal dari penggabungan persamaan
Cos^2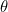 + sin^2
+ sin^2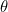 = 1, dan cos^2
= 1, dan cos^2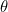 - sin^2
- sin^2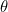 = cos 2
= cos 2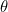 .
.
Apabila kita menjumlahkan dua persamaan untuk mendapatkan 2 cos^2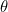 = 1 + cos 2
= 1 + cos 2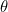 dan mengurangkan persamaan kedua dari persamaan yang pertama untuk mendapatkan 2 sin^2
dan mengurangkan persamaan kedua dari persamaan yang pertama untuk mendapatkan 2 sin^2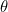 = 1 - cos 2
= 1 - cos 2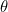 . Ini menghasilkan identitas berikut, yang berguna pada kalkulus integral.
. Ini menghasilkan identitas berikut, yang berguna pada kalkulus integral.
c). Rumus Setengah-Sudut
d). Hukum Kosinus
Jika a, b, dan c adalah sisi segitiga ABC dan jika 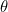 adalah sudut di hadapkan c, maka:
adalah sudut di hadapkan c, maka:
Contoh 1.1
Buktikan!
1. cos (x -  ) = sin x
) = sin x
 ) = sin x
) = sin x
2. sin (x +  ) = cos x
) = cos x
 ) = cos x
) = cos x
3. cos (x +  ) = -sin x
) = -sin x
 ) = -sin x
) = -sin x
4. sin (x -  ) = -cos x
) = -cos x
 ) = -cos x
) = -cos xJawab:
1. cos (x -
 ) = cos x. cos
) = cos x. cos  + sin x. sin
+ sin x. sin 
= cos x . 0 + sin x. 1
= 0 + sin x
= sin x
2. sin (x +
 ) = sin x.cos
) = sin x.cos  + cos x. sin
+ cos x. sin 
= sin x. 0 + cos x. 1
= 0 + cos x
= cos x
3. cos (x +
 ) = cos x. cos
) = cos x. cos  - sin x. sin
- sin x. sin 
= cos x . 0 - sin x. 1
= 0 - sin x
= -sin x
4. sin (x -
 ) = sin x.cos
) = sin x.cos  + cos x. sin
+ cos x. sin 
= sin x. 0 - cos x. 1
= 0 - cos x
= -cos x
Contoh 1.2
Berikut ini adalah contoh rumus setengah sudut. Carilah nilai fungsi berikut!





