Aturan-Aturan Turunan (Diferensiasi) dan Pembuktiannya - Kalkulus
Bachtiarmath.com | pada kesempatan sebelumnya kita sudah membahas tentang cara mencari turunan dengan definisi dan rumus alternatif turunan. Sekarang bachtiarmath.com akan membahas tentang aturan-aturan turunan serta pembuktiannya. Untuk lebih pahamnya, mari simak penjelasan berikut ini.
Dalam turunan terdapat beberapa aturan dalam pengerjaannya, yaitu:
- Aturan pangkat turunan
- Aturan kelipatan konstanta
- Aturan jumlah turunan
- Aturan hasil kali atau perkalian
- Aturan hasil bagi atau pembagian
Berikut ini adalah pembahasan dari kelima aturan-aturan turunan beserta pembuktianya:
1.) Aturan Pangkat
Jika n adalah bilangan real, maka:
Untuk semua x dengan pangkat x^n dan x^n-1 terdefinisi.
2). Aturan Kelipatan Konstanta
Jika u adalah fungsi yang terdiferensiasikan terhadap x, dan c adalah konstanta, maka:
3). Aturan Jumlah Turunan
Jika u dan v fungsi dari x yang terdiferensiasikan, maka jumlah fungsi tersebut u + v terdiferensiakan di setiap titik dimana u dan v keduanya terdiferensiasikan. Pada titik-titik semacam itu.
4). Aturan Hasil Kali Turunan
Jika u dan v terdiferensiasikan di x, maka demikian juga hasil kalinya uv, dan
Bukti dari aturan hasil kali turunan
5). Aturan Hasil Bagi Turunan
Jika u dan v terdiferensiasikan di x dan jika v(x)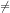 
0, maka hasil bagi u/v juga terdiferensiasikan di x, dan
Bukti dari aturan hasil bagi turunan
Contoh 1.1
Pada soal no 1-5, carilah turunan pertama dan kedua.
Jawab:
Contoh 1.2
Pada soal no 6-8, tentukan turunan pertama dengan menggunakan aturan hasil kali.
Jawab:
Contoh 1.3
Pada soal no 9-13, tentukan turunan pertama menggunakan aturan hasil bagi.
Jawab:
Nomor 13 buat latihan!