Matriks - Pengertian, Jenis, Operasi, Sifat dan Contohnya

Bachtiarmath.com | pada kesempatan kali ini bachtiarmath.com akan mengulas tentang materi matriks lengkap. Materi matriks ini bisa kalian dapatkan di jenjang SMA. Untuk mengatahui apasih matriks? apa saja operasi matriks? apa saja jenis matriks? dan apa saja sifat matriks? mari simak penjelasan berikut ini.

A. Pengertian Matriks

Matriks adalah susunan sekelompok bilangan dalam suatu jajaran berbentuk persegi panjang yang diatur baris dan kolom, serta dibatasi dengan tanda kurung siku atau biasa. Jika matriks tersusun atas m baris dan n kolom, maka dikatakan matriks tersebut ukuran (berordo) m x n. Penulisan matriks biasanya menggunakan huruf kapital dan tebal seperti A, B, C, dan seterusnya. Sedangkan, penulisan matriks beserta ukurannya ( matriks dengan m baris dan n kolom ) adalah  dan seterusnya. (Bandar Lampung, Dona Dinda Pratiwi M.Pd, 2017, cet.I)

Bentuk Umum dari  adalah:

 disebut elemen A yang terletak pada baris i dan kolom j.

B. Jenis-Jenis Matriks

1). Matriks Bujur Sangkar

Matriks bujur sangkar atau persegi adalah matriks yang jumlah barisnya sama dengan jumlah kolomnya. Dalam matriks bujur sangkar dikenal istilah elemen diagonal yang berjumlah n untuk matriks bujur sangkar yang berukuran nxn, yaitu a11, a22, ..., ann.

Contoh:

dengan elemen diagonal a11 dan a22.

dengan elemen diagonal a11 , a22 dan a33.

2). Matriks Baris

Matriks baris adalah matriks yang terdiri dari beberapa baris dan kolom, yang memiliki ordo 1 x n; dengan n > 1.

Contoh:

 disebut matriks baris 1 x 3.
 disebut matriks baris 1 x 4.

3). Matriks Kolom

Matriks kolom adalah matriks yang terdiri dari beberapa baris dan 1 kolom, yang memiliki ordo m x 1; dengan m > 1.

Contoh:

Matriks A disebut matriks kolom 3 x 1.

Matriks B disebut matriks kolom 4 x 1.

4). Matriks Nol

Matriks nol adalah matriks berordo m x n yang elemen-elemennya bernilai 0.

Contoh:

5). Matriks Diagonal

Matriks diagonal adalah matriks yang elemen selain diagonalnya bernilai nol. Dalam hal ini tidak disyaratkan bahwa elemen diagonal harus tak nol.

Contoh:

6). Matriks Segitiga

Matriks segitiga adalah matriks bujur sangkar /persegi yang elemen-elemen dibawah atau diatas elemen diagonal bernilai nol. Jika yang bernilai nol adalah elemen-elemen dibawah elemen diagonal maka disebut matriks segitiga atas, dan sebaliknya jika yang bernilai nol adalah elemen-elemen diatas elemen diagonal maka disebut matriks segitiga bawah. Dalam hal ini, juga tidak disyaratkan bahwa elemen diagonal harus bernilai tak nol.

Contoh:

Matriks A adalah matriks segitiga atas.

Matriks B adalah matriks segitiga bawah.

Matriks C adalah matriks segitiga atas dan matriks segitiga bawah.

7). Matriks Identitas

Matriks identitas adalah matriks diagonal yang elemen diagonalnya bernilai 1.

Contoh:

8). Matriks Simetri

Matriks A disebut matriks simetri, jika matriks tersebut berbentuk bujur sangkar dan .

Contoh:

9). Matriks Simetri Miring

Sebuah matriks A disebut matriks simetri miring jika .

Contoh:

10). Matriks Skalar

Matriks Skalar adalah matriks diagonal yang semua entri pada diagonal utamanya bernilai sama, tetapi tidak nol.

Contoh:

C. Operasi-operasi Matriks

1). Penjumlahan Matriks

Operasi penjumlahan matriks dapat dilakukan pada dua buah matriks yang memiliki ukuran yang sama (ordo sama). Aturan penjumlahan matriks yaitu dengan menjumlahkan elemen-elemen yang bersesuaian pada kedua matriks. Berikut adalah cara menghitung matriks pada penjumlahan matriks:

Bentuk umum:

Contoh:

Diketahui matriks A dan matriks B. Tentukan A+B!


Jawab:

2). Pengurangan Matriks

Operasi pengurangan matriks dapat dilakukan pada dua buah matriks yang memiliki ukuran yang sama (ordo sama). Aturan pengurangan matriks yaitu dengan mengurangkan elemen-elemen yang bersesuaian pada kedua matriks. Berikut cara mengerjakan matriks pada pengurangan matriks:

Bentuk umum:

Contoh:

Diketahui matriks A dan matriks B. Tentukan A-B!

Jawab:




3). Perkalian Matriks dengan Matriks

Perkalian matriks dapat dilakukan pada dua buah matriks yaitu jika jumlah kolomnya matriks A = jumlah baris matriks A.

Aturan perkalian matriks yaitu misalkan dimana elemen-elemen dari C (Cij) merupakan penjumlahan dari perkalian elemen-elemen A baris i dengan elemen-elemen B kolom j.

Bentuk umum 1

Bentuk umum 2

Diatas terdapat 2 versi bentuk umum, namun jangan bingung itu hanyalah untuk referensi saja. Perlu diingat, inti dari perkalian 2 matriks adalah kita harus mengalikan baris dengan kolom. Berikut cara menyelesaikan matriks pada perkalian matriks:

Contoh 1.1

Diketahui matriks A dan matriks B. Tentukan AB dan BA!

Jawab:

Jadi, pada permasalahan diatas dapat disimpulkan bahwa AB 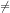 BA.

Contoh 1.2

Buktikan apakah benar sifat asosiatif berlaku pada perkalian matriks yaitu (AB)C=A(BC)!

Jawab:

Jadi, sifat asosiatif berlaku pada perkalian matriks yaitu (AB)C=A(BC)

4). Perkalian Matriks dengan Skalar

Suatu matriks dapat dikalikan suatu skalar k  dengan aturan tiap-tiap elemen pada A dikalikan dengan k.

Bentuk umum:

Contoh:

Diketahui: k = 3, dan matriks A sebagai berikut tentukan kA!

Jawab:

5). Trase Matriks

Misalkan A = [aij] dengan i = 1, 2, 3, ..., n dan j = 1, 2, 3, ..., n. Trase dari matriks A dinyatakan oleh trase (A), dan pada trase mmatriks ini mempunyai syarat yaitu harus matriks bujur sangkar.

Bentuk umum:

Trase A = a + e + i

Cara mencari trase dalam sebuah matriks sangatlah mudah, yaitu hanya menambahkan semua entri diagonal utama (diagonal utamanya sudah saya warnai yaitu yang berwarna biru).

Contoh:

Diketahui matrik A dibawah ini. Hitunglah trase A!

Jawab:

Trase A = 1 + (-3) + 5 = 3

6). Transpose Matriks

Transpose matriks A dinotasikan . Transpose matriks A didefinisikan sebagai matriks yang baris-barisnya merupakan kolom dari A.

Contoh:

7). Matriks Invers

Jika matriks A, dan matriks B adalah matriks bujur sangkar dan berlaku AB = BA = I (I adalah matriks identitas), maka dikatakan bahwa matriks A dapat dibalik dan matriks B adalah matriks invers dari A (dinotasikan ).

Invers Matriks 2x2

Invers Matriks 3x3

D. Sifat-sifat Operasi Matriks

1). Penjumlahan Matriks dan Perkalian dengan Skalar

1. A + B = B + A  {Sifat komutatif)
2. (A + B) + C = A + (B + C)   {Sifat asosiatif}
3. A + 0 = 0 + A  {Sifat matriks nol (identitas penjumlahan)}
4. A + (-A) = -A + A = 0   {Sifat negatf matriks}
5. k(A + B) = kA + kB   {Sifat distribusi terhadap skalar k}
6. (k + l)A = kA + lA   {Sifat distribusi terhadap skalar k dan l}
7. (kl)A = k(lA)   {Sifat Asosiatif terhadap perkalian skalar}
8. 1A = A   {Sifat Perkalian dengan sekalar 1 (satu)}

2). Perkalian Matriks

1. A.B  B.A   {Tidak berlaku sifat komutatif}
2. (A.B).C = A.(B.C)   {Sifat asosiatif}
3. AI = IA = A   {Matriks satuan, identitas perkalian}
4. A0 = 0A = 0   {Matriks nol}

3). Transpose dan Trase

Daftar Pustaka

Dinda Pratiwi M.Pd, Dona. (2017). Aljabar Linier, cet.I. CV.Gemilang : Bandar Lampung.

Imrona, Mahmud. (2013). Aljabar Linear Dasar edisi ke-2. Erlangga : Jakarta.

Share this post