Soal dan Pembahasan Program Linear Metode Grafik
Haiii gaes kali ini bachtiarmath.com akan membagikan kumpulan contoh soal dan pembahasan program linear metode grafik yang pernah saya dapatkan pada saat SMA dulu & pada saat perkuliahan.

Pada program linear ini ada beberapa metode yang harus kita kuasai, yaitu antara lain:
- Metode Grafik, dan
- Metode Simplek
Pada materi metode grafik ini terdapat dua fungsi, yaitu fungsi maksimum dan fungsi minimum. Berikut ini adala contoh soal dan pembahasannya:
Soal 1
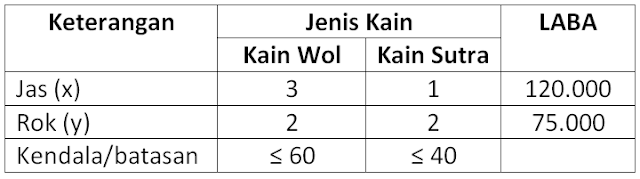
Seorang penjahit mempunyai 60 meter kain wol dan 40 meter kain sutra, dengan bahan yang tersedia penjahit membuat setelan Jas dan Rok untuk beberapa orang pelanggannya. 1 stel Jas memerlukan 3 meter kain wol dan 1 meter kain sutra. Kemudian 1 stel Rok memerlukan 2 meter kain wol dan 2 meter kain sutra. Pendapatan setiap stel Jas dan Rok yaitu Rp. 120.000 dan Rp. 75.000. Berapakah maksimum laba yang didapatkan?
Pembahasan:
Variabel keputusan, misalkan:
- x = Jas
- y = Rok
Fungsi tujuan:
- 120.000x + 75.000y
Fungsi kendala:
- 3x + 2y ≤ 60
- x + 2y ≤ 40
- x, y ≥ 0
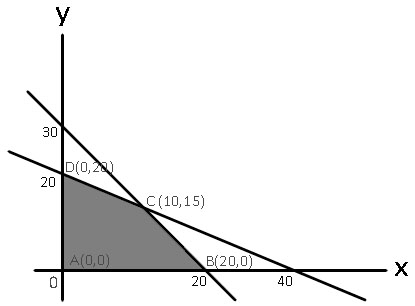
Mencari titik koordinat:
3x + 2y ≤ 60
x = 0, y = 30. Didapat koordinat (0, 30)
y = 0, x = 20. Didapat koordinat (20, 0)
x + 2y ≤ 40
x = 0, y = 20. Didapat koordinat (0, 20)
y = 0, x = 40. Didapat koordinat (40, 0)
Mencari titik potong:
3x + 2y ≤ 60
x + 2y ≤ 40 -
2x ≤ 20
x ≤ 20/2
x ≤ 10
x + 2y ≤ 40
10 + 2y ≤ 40
2y ≤ 40 - 10
y ≤ 30/2
y ≤ 15
Didapatkan titik potong: (10, 15)
Daerah penyelesaiannya:
Mencari nilai maksimum menggunakan titik pojok:

Jadi, laba maksimum yang didapatkan oleh penjahit adalah Rp.2.400.000,00
Soal 2
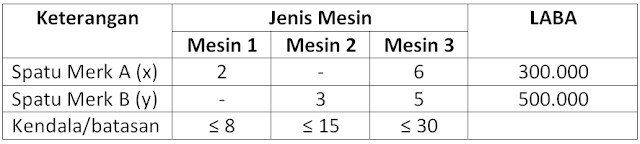
Pabrik sepatu bata membuat dua macam sepatu, masing-masing Merk A dan Merk B untuk membuat sepatu perusahaan memiliki 3 mesin, yaitu mesin 1, 2, dan 3. Sepatu Merk A mula-mula dikerjakan di mesin 1 selama 2 jam tanpa melalui mesin 2 terus dikerjakan dimesin 3 selama 6 jam. Untuk sepatu Merk B tidak diproses di mesin 1 tetapi langsung dikerjakan di mesin 2 selama 3 jam kemudian di mesin 3 selama 5 jam. Jam kerja maksimum setiap hari untuk mesin 1, 8 jam. Dimesin 2, 15 jam. Dimesin 3, 30 jam. Kemudian keuntungan terhadap merk sepatu A sebesar Rp. 300.000 dan sepatu merk B sebesar Rp. 500.000. Berapakah keuntungan maksimum yang didapatkan?
Pembahasan:
Variabel keputusan, misalkan:
- x = sepatu merk A
- y = sepatu merk B
Fungsi tujuan:
- 300.000x + 500.000y
Fungsi kendala:
- 2x ≤ 8
- 3y ≤ 15
- 6x + 5y ≤ 30
- x, y ≥ 0
2x ≤ 8
x ≤ 8/2
x ≤ 4
3y ≤ 15
y ≤ 15/3
y ≤ 5
6x + 5y ≤ 30
x = 0, y = 6. Didapat koordinat (0, 6)
y = 0, x = 5. Didapat koordinat (5, 0)
x ≤ 4
3y ≤ 15
y ≤ 15/3
y ≤ 5
6x + 5y ≤ 30
x = 0, y = 6. Didapat koordinat (0, 6)
y = 0, x = 5. Didapat koordinat (5, 0)
Mencari titik potong ke-1:
2x ≤ 8
x ≤ 8/2
x ≤ 4
6x + 5y ≤ 30
6(4) + 5y ≤ 30
24 + 5y ≤ 30
5y ≤ 30 - 24
5y ≤ 6
y ≤ 6/5
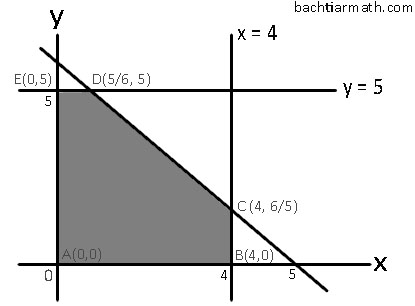
Didapat titik potong: (4, 6/5)
Mencari titik potong ke-2:
3y ≤ 15
y ≤ 15/3
y ≤ 5
6x + 5y ≤ 30
6x + 5(5) ≤ 30
6x + 25 ≤ 30
6x ≤ 30 - 25
6x ≤ 5
x ≤ 5/6
Didapat titik potong: (5/6, 5)
Daerah penyelesaiannya:

Fungsi tujuan:
x + y ≤ 8
x = 0, y = 8. Didapat koordinat (0, 8)
y = 0, x = 8. Didapat koordinat (8, 0)
3x + 4y ≥ 30
x = 0, y = 7,5. Didapat koordinat (0, 7,5)
y = 0, x = 10. Didapat koordinat (10, 0)
x + y ≤ 8 x3
3x + 3y ≤ 24
3x + 4y ≤ 30 -
-y ≤ -6
x + y ≤ 8
x + 6 ≤ 8
x ≤ 8 - 6
x ≤ 2

3x + 2y ≥ 50 x2
6x + 4y ≥ 100 -
-4x ≥ -60

2x ≤ 8
x ≤ 8/2
x ≤ 4
6x + 5y ≤ 30
6(4) + 5y ≤ 30
24 + 5y ≤ 30
5y ≤ 30 - 24
5y ≤ 6
y ≤ 6/5
Didapat titik potong: (4, 6/5)
Mencari titik potong ke-2:
3y ≤ 15
y ≤ 15/3
y ≤ 5
6x + 5y ≤ 30
6x + 5(5) ≤ 30
6x + 25 ≤ 30
6x ≤ 30 - 25
6x ≤ 5
x ≤ 5/6
Didapat titik potong: (5/6, 5)
Daerah penyelesaiannya:

Mencari nilai maksimum menggunakan titik pojok:

Jadi, keuntungan maksimum yang didapat adalah sebesar Rp. 2.750.000 dengan memproduksi sepatu merk A sebanyak 5/6 lusin dan sepatu merk B sebanyak 5 pasang.
Soal 3
Seorang petani memiliki lahan pertanian seluas 8 hektar. Dia akan menanam lahan tersebut dengan tanaman padi dan jagung. Dari 1 hektar tanaman padi dapat dipanen 3 ton padi. Sedangkan dari 1 hektar tanaman jagung dapat dipanen tidak kurang dari 30 ton. Jika biaya menanam 1 hektar tanaman padi Rp. 500.000 dan biaya menanam tanaman 1 hektar jagung Rp. 600.000. Maka biaya minimum yang digunakan adalah sebesar?
Pembahasan:
Variabel keputusan, misalkan:
- x = tanaman padi
- y = tanamann jagung

Fungsi tujuan:
- 500.000x + 600.000y
Fungsi kendala:
- x + y ≤ 8
- 3x + 4y ≥ 30
- x, y ≥ 0
Mencari titik koordinat:
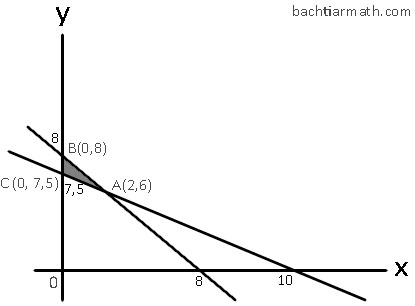
x + y ≤ 8
x = 0, y = 8. Didapat koordinat (0, 8)
y = 0, x = 8. Didapat koordinat (8, 0)
3x + 4y ≥ 30
x = 0, y = 7,5. Didapat koordinat (0, 7,5)
y = 0, x = 10. Didapat koordinat (10, 0)
Mencari titik potong:
3x + 4y ≤ 30 x1
3x + 4y ≤ 30 -
-y ≤ -6
y ≤ 6
x + y ≤ 8
x + 6 ≤ 8
x ≤ 8 - 6
x ≤ 2
Didapat titik potong: (2, 6)
Daerah penyelesaiannya:

Mencari nilai maksimum menggunakan titik pojok:

Jadi, biaya minimum yang harus dikeluarkan petani adalah sebesar Rp. 4.500.000 dengan menaman jagung seluas 7,5 hektar.
Soal 4
Vitamin A dan B ditemukan dalam dua makanan yang berbeda m1 dan m2. Jumlah vitamin disetiap makanan diberikan oleh penjelasan berikut ini:
Fungsi tujuan:
- 1 unit m1 mengandung 2 unit vitamin A dan 3 unit vitamin B, sedangkan 1 unit m2 mengandung 4 unit vitamin A dan 2 unit vitamin B. Keperluan sehari-hari akan vitamin A paling sedikit 40 unit dan vitamin B 50 unit.
- Tujuan kita adalah menentukan jumlah optimal makanan m1 dan m2, sehingga keperluan vitamin A dan B seharinya terpenuhi dengan biaya serendah mungkin. Biaya per unit makanan m1 dan m2 sama dengan Rp. 3.000 dan Rp. 2.500. Berapakah biaya yang diperlukan untuk itu?
Pembahasan:
Variabel keputusan, misalkan:
- x = jenis makanan m1
- y = jenis makanan m2

Fungsi tujuan:
- 3.000x + 2.500y
Fungsi kendala:
- 2x + 4y ≥ 40
- 3x + 2y ≥ 50
- x, y ≤ 0
Mencari titik koordinat:
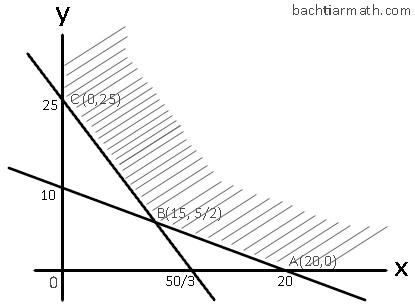
2x + 4y ≥ 40
2x + 4y ≥ 40
x = 0, y = 10. Didapat koordinat (0, 10)
y = 0, x = 20. Didapat koordinat (20, 0)
3x + 2y ≥ 50
x = 0, y = 25. Didapat koordinat (0, 25)
y = 0, x = 50/3. Didapat koordinat (50/3, 0)
Mencari titik potong:
2x + 4y ≥ 40 x1
2x + 4y ≥ 40
-4x ≥ -60
x ≥ -60/-4
x ≥ 15
2x + 4y ≥ 40
2(15) + 4y ≥ 40
30 + 4y ≥ 40
4y ≥ 40 - 30
y ≥ 10/4
y ≥ 5/2x ≥ 15
2x + 4y ≥ 40
2(15) + 4y ≥ 40
30 + 4y ≥ 40
4y ≥ 40 - 30
y ≥ 10/4
Didapat titik potong: (15, 5/2)
Daerah penyelesaiannya:

Mencari nilai maksimum menggunakan titik pojok:

Jadi, biaya manimum yang dikeluarkan adalah sebesar Rp. 51.250 dengan vitamin A sebanyak 15 dan vitamin B sebanyak 5/2.

0 Response to "Soal dan Pembahasan Program Linear Metode Grafik"
Post a Comment