Grup dan Subgrup - Struktur Aljabar I
Misalkan G himpunan tak kosong dan  operasi yang didefinisikan pada G.
operasi yang didefinisikan pada G. 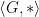 dinamakan grub apabila:
dinamakan grub apabila:
1. Operasi  bersifat tertutup
bersifat tertutup
2. Operasi  bersifat asosiatif
bersifat asosiatif
3. Terdapat e ∈ G sehingga e  x = x
x = x  e = x, untuk setiap x ∈ G. (dentitas)
e = x, untuk setiap x ∈ G. (dentitas)
4. Untuk setiap a ∈ G terdapat a ∈ G dengan sifat a'  a = a
a = a  a' = e. (Invers)
a' = e. (Invers)
Keterangan:
e = elemen netral atau elemen identitas.
a = invers dari a (simbol 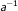 )
)
Definisi 2
Grub 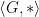 dinamakan grub abelian (komutatif) apabila a
dinamakan grub abelian (komutatif) apabila a  b = b
b = b  a untuk setiap a,b ∈ G.
a untuk setiap a,b ∈ G.
dan juga harus memenuhi ke-4 sifat pada definisi 1.
Contoh:
Didefinisikan operasi  pada
pada 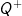 dengan a
dengan a  b =
b = 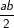 . Buktikan bahwa
. Buktikan bahwa 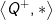 grub abelian!
grub abelian!
Jawab:
1. Adib  bersifat tertutup
bersifat tertutup
Ambil sembarang a,b ∈ 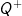 .
.
Jelas a  b =
b = 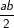 ∈
∈ 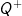 .
.
Jadi bersifat tertutup.
2. Adib  bersifat asosiatif
bersifat asosiatif
Ambi sembarang a,b,c 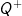 .
.
Karena (a b)
b) c = a
c = a (b
(b c) maka operasi
c) maka operasi  bersifat asosiatif.
bersifat asosiatif.
3. Adib mempunyai elemen netral (Identitas)
Ambil sembarang a ∈ 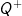 .
.
Karena a e = e
e = e a = a maka operasi
a = a maka operasi  bersifat identitas atau mempunyai elemen netral.
bersifat identitas atau mempunyai elemen netral.
4. Adib mempunyai invers
Ambil sembarang a ∈ 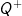 .
.
Jadi setiap a ∈ 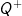 mempunyai invers
mempunyai invers 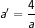
5. Adib  bersifat komutatif
bersifat komutatif
Ambil sembarang a,b ∈ 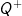 .
.
Karena a b = b
b = b a maka operasi
a maka operasi  bersifat komutatif.
bersifat komutatif.
Berdasarkan 1, 2, 3, 4, dan 5 dapat disimpulkan bahwa 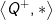 merupakan grub abelian.
merupakan grub abelian.
B. Subgrub
Definisi
Jika G grub dan H ⊂ G maka H dinamakan subgrub apabila H merupakan grub terhadap operasi yang didefinisikan pada G.
Teorema
Diketahui G grub dan H ⊂ G. H subgrub G jika dan hanya jika
1. H bersifat tertutup terhadap operasi pada G.
2. e ∈ H.
3.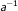 ∈ H untuk setiap a ∈ H.
∈ H untuk setiap a ∈ H.
Materi diatas diambil dari jurnal pdf Buku Ajar Penghantar Struktur Aljabar 1 yang dibuat oleh Isnarto, S.Pd, M.Si. Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Semarang. Tahun 2008.
Baca Juga:
B. Subgrub
Definisi
Jika G grub dan H ⊂ G maka H dinamakan subgrub apabila H merupakan grub terhadap operasi yang didefinisikan pada G.
Teorema
Diketahui G grub dan H ⊂ G. H subgrub G jika dan hanya jika
1. H bersifat tertutup terhadap operasi pada G.
2. e ∈ H.
3.
Materi diatas diambil dari jurnal pdf Buku Ajar Penghantar Struktur Aljabar 1 yang dibuat oleh Isnarto, S.Pd, M.Si. Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Semarang. Tahun 2008.
Baca Juga:


0 Response to "Grup dan Subgrup - Struktur Aljabar I"
Post a Comment