Kumpulan Soal Grup dan Subgrup - Struktur Aljabar I
 |
| https://www.pixabay.com |
1. Didefinisikan operasi
2. Didefinisikan operasi  pada
pada 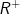 dengan a
dengan a  b =
b = 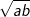 .
.
3. Operasi  pada Z dengan a
pada Z dengan a  b = 2a - b.
b = 2a - b.
Jawaban soal no 1
1. Adib  bersifat tertutup
bersifat tertutup
Ambil sembarang a,b ∈ R .
.
Jelas a  b =
b = 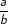 ∈ R
∈ R
Jadi bersifat tertutup.
2. Adib  bersifat asosiatif
bersifat asosiatif
Ambil sembarang a,b,c ∈ R .
.
Karena (a
Karena operasi asosiatif tidak terpenuhi maka dapat disimpulkan bahwa
Jawaban soal no 2
1. Adib  bersifat tertutup
bersifat tertutup
Ambil sembarang a,b ∈ 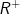 .
.
Jelas a  b =
b = 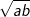 ∈
∈ 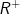
Jadi bersifat tertutup.
2. Adib  bersifat asosiatif
bersifat asosiatif
Ambil sembarang a,b,c ∈ 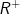 .
.
Karena (a
Karena operasi asosiatif tidak terpenuhi maka dapat disimpulkan bahwa
Jawaban soal no 3
1. Adib  bersifat tertutup
bersifat tertutup
Ambil sembarang a,b ∈ Z.
Jelas a  b = 2a - b ∈ Z.
b = 2a - b ∈ Z.
Jadi bersifat tertutup.
2. Adib  bersifat asosiatif
bersifat asosiatif
Ambil sembarang a,b,c ∈ Z.
\ast&space;c=(2a-b)\ast&space;c\\\\&space;~~~~~~~~~~~~~~~~~~~~~~~~~=2.(2a-b)-c\\\\&space;~~~~~~~~~~~~~~~~~~~~~~~~~=4a-2b-c)
=a\ast&space;(2b-c)\\\\&space;~~~~~~~~~~~~~~~~~~~~~~~~~=2a-(2b-c)\\\\&space;~~~~~~~~~~~~~~~~~~~~~~~~~=2a-2b+c)
Karena operasi asosiatif tidak terpenuhi maka dapat disimpulkan bahwa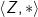 bukan merupakan grub.
bukan merupakan grub.
Karena (a b)
b) c ≠ a
c ≠ a (b
(b c) maka operasi
c) maka operasi  tidak bersifat asosiatif.
tidak bersifat asosiatif.
Karena operasi asosiatif tidak terpenuhi maka dapat disimpulkan bahwa

0 Response to "Kumpulan Soal Grup dan Subgrup - Struktur Aljabar I"
Post a Comment