Operasi Biner - Struktur Aljabar I
Pada kesempatan ini bachtiarmath.com akan membahaas tentang materi lanjutan dari relasi ekuivalen, yaitu materi operasi biner. Penasaran bagaimana cara mengerjaan soal operasi biner, mari simak penjelasan berikut ini.
Definisi 1
 |
| https://www.pixabay.com |
S suatu himpunan operasi biner 
(a, b) ∈ SxS, → n ∈ S.
Contoh:
1. Operasi Penjumlahan
Operasi + pada R merupakan operasi biner.
(2, 3) = 5
(3, 4) = 7
(3, 5) = 8
dan sebagainya
2. Operasi Pembagian
Operasi pembagian (:) pada Z bukan merupakan operasi biner. Sebab (3, 5) ∈ Z, tetapi 3:5=3/5 ∉ Z.
Definisi 2
Operasi  pada S dikatakan:
pada S dikatakan:
1. Komutatif, jika a  b = b
b = b  a untuk setiap a,b ∈ S.
a untuk setiap a,b ∈ S.
2. Asosiatif, jika (a b)
b) c = a
c = a (b
(b c) untuk setiap a,b,c ∈ S.
c) untuk setiap a,b,c ∈ S.
Contoh 1.1
Operasi  pada R* = R-{0} (dibaca R tak nol) a
pada R* = R-{0} (dibaca R tak nol) a  b =
b = 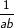 . Berikut ini adalah pembahasannya:
. Berikut ini adalah pembahasannya:
1). Adib
Ambil sembarang a,b ∈ R*
Jadi
2). Adib
Ambil sembarang a,b,c ∈ R*
Karena, (a b)
b) c ≠ a
c ≠ a (b
(b c) maka operasi
c) maka operasi  tidak bersifat asosiatif.
tidak bersifat asosiatif.
Contoh 1.2
Operasi
1). Adib  bersifat komutatif
bersifat komutatif
Ambil sembarang a,b ∈ Z-{0}.
b  a = (ba) + 2
a = (ba) + 2
Karena, a  b = b
b = b  a maka operasi
a maka operasi  bersifat komutatif.
bersifat komutatif.
2). Adib  bersifat asosiatif
bersifat asosiatif
Ambil sembarang a,b,c ∈ Z-{0}.
Karena, (a
Materi diatas diambil dari jurnal pdf Buku Ajar Penghantar Struktur Aljabar 1 yang dibuat oleh Isnarto, S.Pd, M.Si. Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Semarang. Tahun 2008.
Pada soal dibawah ini. Selidiki apakah operasi
1. Operasi
2. Operasi  pada Z dengan a
pada Z dengan a  b = 2a + b + 2.
b = 2a + b + 2.
3. Didefinisikan  pada
pada 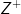 dengan a
dengan a  b =
b = 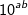
4. Didefinisikan  pada Q dengan a
pada Q dengan a  b = a.(b+1)
b = a.(b+1)

0 Response to "Operasi Biner - Struktur Aljabar I"
Post a Comment