Kumpulan Soal Grup Siklik - Struktur Aljabar I
 |
| https://www.pixabay.com |
1. Cari grub siklik berikut ini
2. Cari grub siklik berikut ini
Jawaban No 1
Invers dari
1. Untuk a =
Diperoleh:
Ternyata {
Jadi,
2. Untuk a =
Diperoleh:
Ternyata {
Jadi,
3. Untuk a =
Diperoleh:
Ternyata {
Jadi,
Kesimpulan:
Subgrup di
- {
} siklik dengan generator
.
- {
,
,
,
,
,
,
} siklik dengan generator
,
,
,
,
, dan
.
Jawaban No 2
Cara mengerjakan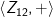 sama dengan pengerjaan
sama dengan pengerjaan 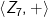 . Saya tidak menggunakan proses, karena prosesnya terlalu panjang, jadi tidak sempat menulis. Namun jangan kawatir saya akan memberikan kesimpulannya untuk mempermudah.
. Saya tidak menggunakan proses, karena prosesnya terlalu panjang, jadi tidak sempat menulis. Namun jangan kawatir saya akan memberikan kesimpulannya untuk mempermudah.
Invers dari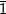 adalah
adalah 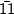
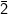 adalah
adalah 
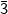 adalah
adalah 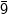
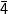 adalah
adalah 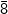
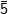 adalah
adalah 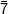
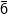 adalah
adalah 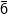
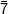 adalah
adalah 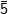
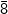 adalah
adalah 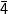
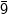 adalah
adalah 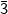
 adalah
adalah 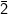
Cara mengerjakan
Invers dari
1. Untuk a = 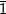
Diperoleh: grup siklik
2. Untuk a = 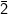
Diperoleh: tidak siklik
3. Untuk a = 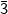
Diperoleh: tidak siklik
4. Untuk a = 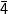
Diperoleh: tidak siklik
5. Untuk a = 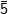
Diperoleh: grup siklik
6. Untuk a = 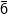
Diperoleh : tidak siklik
Kesimpulan:
bukan generator
, karena
∈ Z, tetapi ∄n ∈ Z sehingga (
)^n =
.
bukan generator
, karena
∈ Z, tetapi ∄n ∈ Z sehingga (
)^n =
.
bukan generator
, karena
∈ Z, tetapi ∄n ∈ Z sehingga (
)^n =
.
bukan generator
, karena
∈ Z, tetapi ∄n ∈ Z sehingga (
)^n =
.
Subgrup di 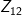
- {
} siklik dengan generator
- {
,
,
,
,
} siklik dengan generator
atau
- {
,
,
,
} siklik dengan generator
atau
- {
,
,
} siklik dengan generator
atau
- {
,
} siklik dengan generator
Semoga Bermanfaat Gaesss...

0 Response to "Kumpulan Soal Grup Siklik - Struktur Aljabar I"
Post a Comment